資産運用基礎講座シリーズ

債券実務編（第４回）：イールドカーブ理論

トータル・ポートフォリオ・ソリューション本部長、エグゼクティブコンサルタント　金武伸治

長期金利は短期金利の「累積」

2024年7月末現在、米国やドイツなど主要先進国の国債イールドカーブ（残存年数ごとの国債利回りを繋いだ利回り曲線）は逆イールド、つまり短期金利よりも長期金利の方が低い形状をしています。これはリスク・フリーレートに近い短期金利よりも、長期の金利リスクを負うことにより、そのリスクへの対価（プレミアム）が求められる長期金利の方が低い（金利リスクに対するプレミアムがマイナス）状態を意味していることから、異常な形状であるとも言えます。そもそも、なぜイールドカーブは右肩上がり（これを、逆イールドに対して順イールドといいます）でないといけないのでしょうか？

加えて、現在の日本国債のイールドカーブは中期部分が凹んだ形状、つまり下に凸な状態になっています。こちらも一般的なイールドカーブのイメージとは異なります。

イールドカーブが現在の歪んだ状態から、長期的にはどのような形状に回帰するのか。このようなことを考える際にも、理論的なあるべき姿を知っておくことは重要です。またヘッジ外債投資を継続するべきか否かなど、長期的な投資戦略を考えるうえでも重要となります。

このため今回は通常の実務編とは少し離れて、「理論的なイールドカーブは、どのように推定されるのか？」というテーマにチャレンジしたいと思います。

理論的なイールドカーブの考え方

はじめに理論イールドカーブの推定方法について説明します。ファイナンス理論では、長期金利とは「現在から将来までの各時点の短期金利の累積」と定義されています。例えば10年金利の場合、現在から10年分の将来短期金利を累積させることで推定しようとしているのです。

現在の短期金利とは、日本の場合ですと政策金利である無担保コール翌日物金利として既に値が決まっています。しかし将来の短期金利は不確実ですし、予想も人それぞれ異なります。では将来の短期金利はどのように設定するのでしょうか？

実は、将来のことは分からないという前提に立ち、各時点の短期金利はランダムに動くという考え方をしています。ただし過度に変動しても困るので、ある時点の短期金利水準から次の時点までは、短期金利の変動分布、つまり標準偏差に従う程度の幅でランダムに上下動させています。

さらに将来の短期金利水準が極端に大きな値やマイナス値にならないように、長期的な均衡水準に回帰するような調整もしています。長期的な均衡水準とは、中立金利（名目ベース。実質ベースでは自然利子率：Rスター）などが挙げられます。つまり経済成長率にふさわしい、景気を加速も減速もさせない適正な政策金利くらいであると理解すると適当です。

【将来短期金利の推定方法例】

ボラティリティ：短期金利変化の標準偏差
乱数：標準正規分布（平均=0、分散=1の正規分布）に従う乱数。概ね-2～+2で変動
調整項：ある時点の短期金利が、長期的な均衡水準よりも高い場合はマイナス方向の調整、低い場合はプラス方向の調整を行う項
出所：ラッセル・インベストメント作成

【図表１】将来の短期金利がランダムに変動する様子（※イメージ図）

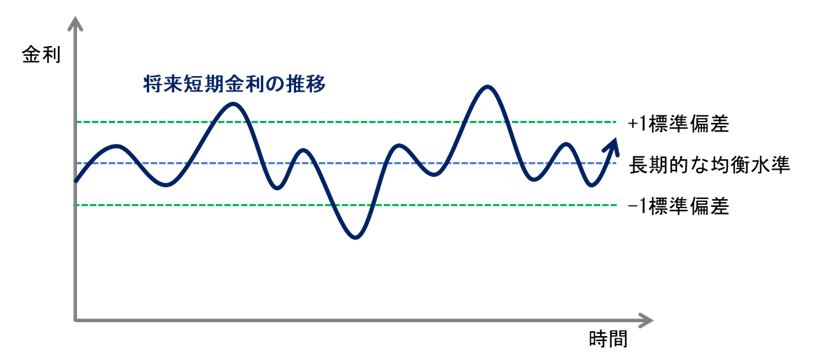
出所　ラッセル・インベストメント作成

長期金利には長短金利差（ターム・プレミアム）を上乗せ

しかしこの場合、将来短期金利は均衡水準を中心にして、正規分布に従い上下動しているだけなので、それを中期や長期、超長期まで累積させても、年率換算すると結局は均衡水準と同等程度になります。つまりイールドカーブが右肩上がりにはならず平坦になってしまいます。

そこで将来の短期金利は不確実なので、長期金利には不確実性に対する対価、つまりリスク・プレミアム（上乗せ金利）を乗せながら累積していきます。これによって、イールドカーブが右肩上がりの形状になる訳です。この短期金利に対して長期金利の期間的（ターム）な不確実性に対する対価を、ターム・プレミアムと呼びます。

ここで、リスク・プレミアムについて補足しておきます。例えば株式の場合、理論株価はその企業の将来の配当を現在価値に割り引いた値の合計となります。そして現在価値に割り引く際に、事業リスクつまりボラティリティが高い企業は高い利回りで割り引く（現在価値が低く割安になる）。またボラティリティが低い企業は低い利回りで割り引く（現在価値が高く割高になる）ことになります。つまりボラティリティの高低によってリスク・プレミアムの大小が変わってきます。イールドカーブについても、金利ボラティリティの高さに応じたリスク・プレミアムを推定することが一般的です。

コンベクシティとは

ターム・プレミアム、つまり残存年数に応じた上乗せ金利は、デュレーション・リスクに応じたプレミアムと言えます。このターム・プレミアムの存在により、イールドカーブは右肩上がりの形状をしています。つまり「傾き」を持っているということです。一方で、一般的なイールドカーブは中期部分が膨らんだ形状をしています。つまり上に凸となる曲率を持っているということです。そして「傾き」はデュレーションと関係していましたが、「曲率」はコンベクシティというものに関係しています。

デュレーションとは債券価格の金利感応度であり、金利が1%上昇した際に債券価格が何%下落するかを表す指標でした。つまり金利変化と債券価格変化の関係は、
「債券価格変化＝金利変化×デュレーション」
となり、債券価格が金利変化に比例して変化するということでした。

しかし実際の金利変化と債券価格変化の関係は図表２のように、比例のような直線的ではなく曲線的な関係をしています。

【図表２】金利変化と債券価格変化の関係（※イメージ図）

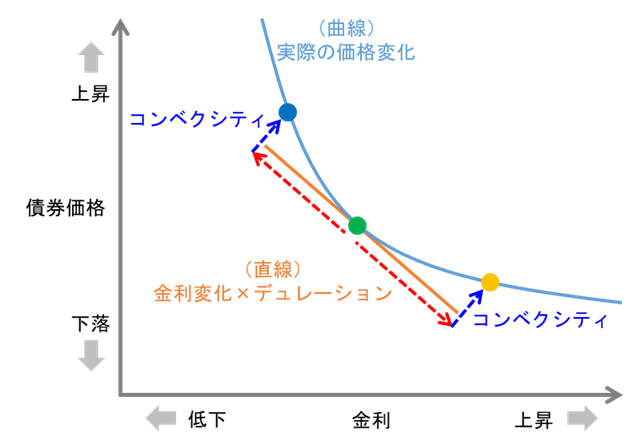
出所　ラッセル・インベストメント作成

ここで金利低下時の債券価格の上昇幅は直線よりも大きく、金利上昇時の価格の下落幅は直線よりも小さいことがわかります。これは同じ1%の金利変化幅でも、金利が低下して低金利になった時には、相対的にその割合は大きくなる（例えば、金利が2%の時の1%の金利変化は50%の変化率となる）ため、金利感応度も上昇する（デュレーションが大きくなる）ためです。逆に金利が上昇して高金利になった時には、相対的に小さくなる（例えば、金利が4%の時の1%の金利変化は25%の変化率となる）ため、金利感応度も低下します（デュレーションが小さくなる）。

このように、曲線で示される実際の価格変化幅と直線で示される価格変化幅の差は常にプラスとなり、これを「コンベクシティ」と呼びます。英語で「convex」が「凸面、凸型」を意味するところから由来しています。簡略化のために理論的な説明は除きますが、コンベクシティは残存年数の2乗に比例して大きくなります。つまり残存年数が5倍になると、デュレーションは概ね5倍になりますが、コンベクシティは5の2乗の25倍になるという性質を持っています。

デュレーションは、金利低下の場合は債券価格の上昇に、金利上昇の場合は債券価格の下落に作用する「リスク」ですが、コンベクシティは、金利が低下しても上昇しても債券価格の上昇に作用する「良いもの」と言えます。

イールドカーブに曲率を実装

これまでの内容を整理します。イールドカーブにおいて、将来短期金利を累積して長期金利が形成されます。将来には不確実性が伴います。このリスクがデュレーション・リスク（金利変動リスク）であり、その対価として長期金利にはターム・プレミアムが乗せられます。このためイールドカーブは右肩上がりの形状となります。つまりイールドカーブの傾きは、デュレーションと関係しています。

イールドカーブには、もう1つの特徴があります。それは上に凸の形状をしていることです。これは短期金利と長期金利の中間である中期金利が、短期金利と長期金利の平均（直線で結んだ水準）よりも高い傾向があることを示しています。

なぜ、中期金利は短期金利と長期金利の平均よりも高いのでしょうか。ここにコンベクシティが関係しています。図表３に、傾きと曲率を持つ、一般的なイールドカーブの形状を示しました。

【図表３】（平常時）上に凸の形状のイールドカーブ（※イメージ図）

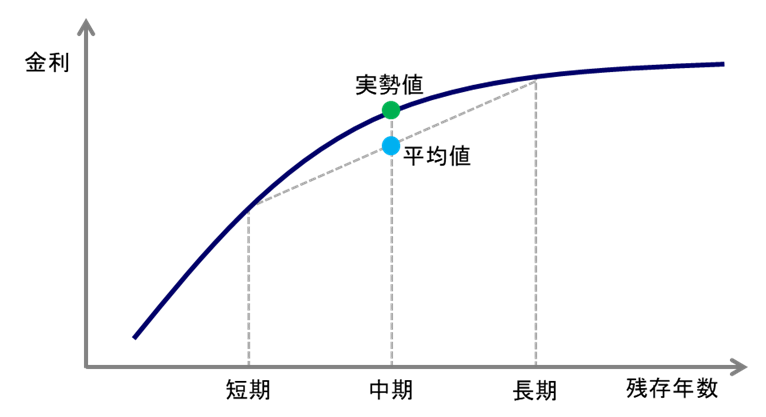
出所　ラッセル・インベストメント作成

先に、コンベクシティは残存年数の2乗に比例して大きくなることを説明しました。ここで、残存年数2年と残存年数10年、そしてその中間の残存年数6年について考えます。相対的な大きさとして、残存年数2年のコンベクシティを4とします。なぜなら2年の2乗が4であるためです。同じく6年のコンベクシティは36（6の2乗）、10年のコンベクシティは100（10の2乗）となります。

ここで、2年と10年の債券を半々で保有するケースと、6年の債券だけを保有するケースを考えます。平均残存年数はどちらも6になります。つまりデュレーション・リスクは概ね同じです。一方でコンベクシティは、2年と10年を半々で保有すると52、6年だけを保有すると36となります。
同じデュレーションであるならコンベクシティが高い方が良いため、2年と10年を半々で保有する方が良くなります。このためコンベクシティが相対的に小さい6年の金利が、2年と10年の平均金利では買い手が付かず、需要の低下によって利回りが高くなります。
つまり短期金利と長期金利の平均よりも中期金利の方が高くなり、イールドカーブの形状が上に凸となる訳です。このようにイールドカーブの曲率は、コンベクシティと関係しているのです。

※本稿では理解の促進を優先して、一部、簡略化・簡易化している部分があります

Recommended reading

FIXED INCOME